what volume is needed to store 0.80 moles of helium gas at 204.6 kpa and 300 k?

Chapter nine. Gases

ix.3 Stoichiometry of Gaseous Substances, Mixtures, and Reactions

Learning Objectives

By the finish of this section, you will be able to:

• Use the ideal gas law to compute gas densities and tooth masses
• Perform stoichiometric calculations involving gaseous substances
• Land Dalton's police force of partial pressures and apply it in calculations involving gaseous mixtures

The study of the chemical beliefs of gases was function of the basis of perhaps the nearly fundamental chemical revolution in history. French nobleman Antoine Lavoisier, widely regarded as the "male parent of modern chemistry," changed chemistry from a qualitative to a quantitative scientific discipline through his piece of work with gases. He discovered the law of conservation of thing, discovered the office of oxygen in combustion reactions, determined the composition of air, explained respiration in terms of chemic reactions, and more. He was a casualty of the French Revolution, guillotined in 1794. Of his death, mathematician and astronomer Joseph-Louis Lagrange said, "It took the mob only a moment to remove his head; a century volition not suffice to reproduce it."^[1]

Equally described in an earlier affiliate of this text, we can turn to chemical stoichiometry for answers to many of the questions that ask "How much?" Nosotros tin answer the question with masses of substances or volumes of solutions. Nevertheless, we can also answer this question some other mode: with volumes of gases. We can use the ideal gas equation to relate the force per unit area, book, temperature, and number of moles of a gas. Here we will combine the ideal gas equation with other equations to find gas density and molar mass. Nosotros will deal with mixtures of different gases, and calculate amounts of substances in reactions involving gases. This department volition not introduce any new textile or ideas, but will provide examples of applications and means to integrate concepts we have already discussed.

Density of a Gas

Recall that the density of a gas is its mass to volume ratio, [latex]\rho = \frac{thousand}{V}[/latex]. Therefore, if we tin determine the mass of some volume of a gas, we will get its density. The density of an unknown gas can used to determine its tooth mass and thereby assistance in its identification. The ideal gas law, PV = nRT, provides us with a means of deriving such a mathematical formula to relate the density of a gas to its book in the proof shown in Example 1.

Example i

Derivation of a Density Formula from the Platonic Gas Law
Use PV = nRT to derive a formula for the density of gas in g/L

Solution

1. PV = nRT
2. Rearrange to get (mol/L): [latex]\frac{due north}{5} = \frac{P}{RT}[/latex]
3. Multiply each side of the equation past the molar mass, [latex]\mathcal{M}[/latex]. When moles are multiplied by [latex]\mathcal{M}[/latex] in 1000/mol, g are obtained:
   [latex](\mathcal{One thousand})(\frac{n}{V}) = (\frac{P}{RT})(\mathcal{Thou})[/latex]
4. [latex]one thousand \text{/L} = \rho = \frac{P \mathcal{M}}{RT}[/latex]

Check Your Learning
A gas was found to have a density of 0.0847 g/L at 17.0 °C and a pressure level of 760 torr. What is its tooth mass? What is the gas?

Answer:

[latex]\rho = \frac{P \mathcal{One thousand}}{RT}[/latex]

[latex]0.0847 \;\text{g/L} = 760 \;\rule[0.5ex]{1.7em}{0.1ex}\hspace{-1.7em}\text{torr} \times \frac{1 \;\rule[0.25ex]{1.2em}{0.1ex}\hspace{-ane.2em}\text{atm}}{760 \;\rule[0.25ex]{1.2em}{0.1ex}\hspace{-1.2em}\text{torr}} \times \frac{\mathcal{M}}{0.0821 \;\text{L} \;\rule[0.25ex]{one.2em}{0.1ex}\hspace{-1.2em}\text{atm/mol Thou}} \times 290 \;\text{K}[/latex]

[latex]\mathcal{M}[/latex] = ii.02 g/mol; therefore, the gas must be hydrogen (H₂, two.02 g/mol)

We must specify both the temperature and the force per unit area of a gas when calculating its density because the number of moles of a gas (and thus the mass of the gas) in a liter changes with temperature or pressure. Gas densities are often reported at STP.

Instance ii

Empirical/Molecular Formula Problems Using the Ideal Gas Constabulary and Density of a Gas
Cyclopropane, a gas once used with oxygen every bit a general anesthetic, is composed of 85.7% carbon and 14.iii% hydrogen by mass. Find the empirical formula. If 1.56 g of cyclopropane occupies a volume of 1.00 Fifty at 0.984 atm and 50 °C, what is the molecular formula for cyclopropane?

Solution
Strategy: First solve the empirical formula problem using methods discussed before. Presume 100 chiliad and convert the percentage of each element into grams. Decide the number of moles of carbon and hydrogen in the 100-g sample of cyclopropane. Divide by the smallest number of moles to relate the number of moles of carbon to the number of moles of hydrogen. In the last step, realize that the smallest whole number ratio is the empirical formula:

[latex]\begin{array}{fifty l}85.7 \;\text{yard C} \times \frac{i \;\text{mol C}}{12.01 \;\text{thousand C}} = 7.136 \;\text{mol C} & \frac{7.136}{vii.136} = 1.00 \;\text{mol C} \\[1em] 14.3 \;\text{g H} \times \frac{1 \;\text{mol H}}{1.01 \;\text{g H}} = xiv.158 \;\text{mol H} & \frac{14.158}{7.136} = ane.98 \;\text{mol H} \terminate{array}[/latex]

Empirical formula is CH₂ [empirical mass (EM) of fourteen.03 g/empirical unit].

Next, use the density equation related to the ideal gas law to make up one's mind the molar mass:

[latex]\text{d} = \frac{P \mathcal{M}}{RT} \;\;\;\;\; \frac{one.56 \;\text{thou}}{1.00 \;\text{50}} = 0.984 \;\text{atm} \times \frac{\mathcal{K}}{0.0821 \;\text{L atm/mol G}} \times 323 \;\text{K}[/latex]

[latex]\mathcal{M}[/latex] = 42.0 g/mol, [latex]\frac{\mathcal{M}}{\text{E} \mathcal{M}} = \frac{42.0}{14.03} = 2.99[/latex], then (3)(CH₂) = C₃H₆ (molecular formula)

Cheque Your LearningAcetylene, a fuel used welding torches, is comprised of 92.3% C and 7.7% H by mass. Discover the empirical formula. If one.10 g of acetylene occupies of volume of ane.00 L at ane.fifteen atm and 59.5 °C, what is the molecular formula for acetylene?

Answer:

Empirical formula, CH; Molecular formula, C_iiH₂

Molar Mass of a Gas

Another useful awarding of the ideal gas law involves the conclusion of molar mass. Past definition, the tooth mass of a substance is the ratio of its mass in grams, m, to its amount in moles, n:

[latex]\mathcal{M} = \frac{\text{grams of substance}}{\text{moles of substance}} = \frac{m}{n}[/latex]

The platonic gas equation tin be rearranged to isolate northward:

[latex]n = \frac{PV}{RT}[/latex]

and then combined with the tooth mass equation to yield:

[latex]\mathcal{M} = \frac{mRT}{PV}[/latex]

This equation can be used to derive the molar mass of a gas from measurements of its pressure, volume, temperature, and mass.

Instance 3

Determining the Molar Mass of a Volatile Liquid
The gauge tooth mass of a volatile liquid tin can be determined past:

1. Heating a sample of the liquid in a flask with a tiny hole at the top, which converts the liquid into gas that may escape through the pigsty
2. Removing the flask from heat at the instant when the final bit of liquid becomes gas, at which fourth dimension the flask volition be filled with only gaseous sample at ambience pressure
3. Sealing the flask and permitting the gaseous sample to condense to liquid, and so weighing the flask to decide the sample's mass (meet Effigy 1)

Figure 1. When the volatile liquid in the flask is heated past its boiling signal, it becomes gas and drives air out of the flask. At t_l⟶1000, the flask is filled with volatile liquid gas at the same pressure as the atmosphere. If the flask is so cooled to room temperature, the gas condenses and the mass of the gas that filled the flask, and is now liquid, can exist measured. (credit: modification of work past Mark Ott)

Using this process, a sample of chloroform gas weighing 0.494 g is collected in a flask with a volume of 129 cm³ at 99.6 °C when the atmospheric pressure is 742.1 mm Hg. What is the estimate molar mass of chloroform?

Solution
Since [latex]\mathcal{M} = \frac{m}{due north}[/latex] and [latex]n = \frac{PV}{RT}[/latex], substituting and rearranging gives [latex]\mathcal{M} = \frac{mRT}{PV}[/latex],

then

[latex]\mathcal{G} = \frac{mRT}{PV} = \frac{(0.494 \;\text{g}) \times 0.08206 \;\text{L} \cdot \text{atm/mol Thou} \times 372.8 \;\text{Chiliad}}{0.976 \;\text{atm} \times \; 0.129 \;\text{L}} = 120 \;\text{chiliad/mol}[/latex]

Check Your Learning
A sample of phosphorus that weighs 3.243 × 10⁻² g exerts a force per unit area of 31.89 kPa in a 56.0-mL bulb at 550 °C. What are the molar mass and molecular formula of phosphorus vapor?

The Pressure of a Mixture of Gases: Dalton'due south Constabulary

Unless they chemically react with each other, the individual gases in a mixture of gases practise not affect each other's force per unit area. Each individual gas in a mixture exerts the same pressure that it would exert if information technology were nowadays lonely in the container (Figure 2). The force per unit area exerted past each individual gas in a mixture is called its partial force per unit area. This observation is summarized by Dalton's law of fractional pressures: The total pressure of a mixture of ideal gases is equal to the sum of the fractional pressures of the component gases:

[latex]P_{Total} = P_A + P_B + P_C + \cdots = \sum_{\text{i}} P_\text{i}[/latex]

In the equation P_Total is the total pressure of a mixture of gases, P_A is the fractional pressure of gas A; P_B is the partial pressure of gas B; P_C is the partial pressure of gas C; and so on.

Figure 2. If equal-book cylinders containing gas A at a pressure level of 300 kPa, gas B at a pressure of 600 kPa, and gas C at a force per unit area of 450 kPa are all combined in the same-size cylinder, the total force per unit area of the mixture is 1350 kPa.

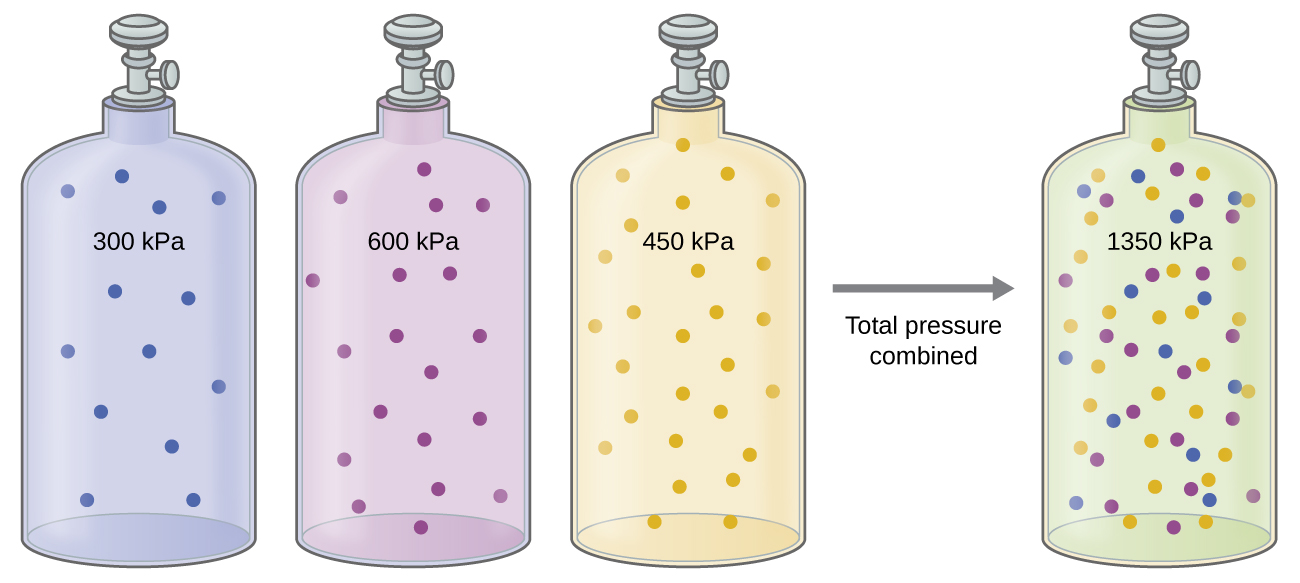
The partial pressure of gas A is related to the total pressure level of the gas mixture via its mole fraction (X), a unit of measurement of concentration defined every bit the number of moles of a component of a solution divided by the total number of moles of all components:

[latex]P_A = X_A \times P_{Total} \;\;\;\;\; \text{where} \;\;\;\;\; X_A = \frac{n_A}{n_{Total}}[/latex]

where P_A , 10_A , and n_A are the fractional pressure level, mole fraction, and number of moles of gas A, respectively, and n_Full is the number of moles of all components in the mixture.

Case 4

The Pressure of a Mixture of Gases
A ten.0-50 vessel contains ii.50 × x⁻³ mol of H_ii, 1.00 × 10^−three mol of He, and 3.00 × 10⁻⁴ mol of Ne at 35 °C.

(a) What are the partial pressures of each of the gases?

(b) What is the full pressure in atmospheres?

Solution
The gases deport independently, so the fractional pressure level of each gas can be adamant from the platonic gas equation, using [latex]P = \frac{nRT}{Five}[/latex]:

[latex]P_{\text{H}_2} = \frac{(two.50 \times x^{-3} \;\rule[0.5ex]{1.2em}{0.1ex}\hspace{-1.2em}\text{mol})(0.08206 \;\rule[0.5ex]{0.5em}{0.1ex}\hspace{-0.5em}\text{L} \;\text{atm} \;\dominion[0.5ex]{3.5em}{0.1ex}\hspace{-three.5em}\text{mol}^{-1} \text{K}^{-1})(308 \;\rule[0.5ex]{0.5em}{0.1ex}\hspace{-0.5em}\text{Yard})}{10.0 \;\rule[0.5ex]{0.5em}{0.1ex}\hspace{-0.5em}\text{Fifty}} = 6.32 \times ten^{-3} \;\text{atm}[/latex]

[latex]P_\text{He} = \frac{(1.00 \times 10^{-3} \;\rule[0.5ex]{1.2em}{0.1ex}\hspace{-ane.2em}\text{mol})(0.08206 \;\dominion[0.5ex]{0.5em}{0.1ex}\hspace{-0.5em}\text{Fifty} \;\text{atm} \;\dominion[0.5ex]{three.5em}{0.1ex}\hspace{-3.5em}\text{mol}^{-1} \text{K}^{-1})(308 \;\dominion[0.5ex]{0.5em}{0.1ex}\hspace{-0.5em}\text{K})}{10.0 \;\dominion[0.5ex]{0.5em}{0.1ex}\hspace{-0.5em}\text{L}} = 2.53 \times 10^{-3} \;\text{atm}[/latex]

[latex]P_\text{Ne} = \frac{(3.00 \times 10^{-4} \;\dominion[0.5ex]{i.2em}{0.1ex}\hspace{-i.2em}\text{mol})(0.08206 \;\rule[0.5ex]{0.5em}{0.1ex}\hspace{-0.5em}\text{L} \;\text{atm} \;\rule[0.5ex]{3.5em}{0.1ex}\hspace{-3.5em}\text{mol}^{-1} \text{K}^{-1})(308 \;\rule[0.5ex]{0.5em}{0.1ex}\hspace{-0.5em}\text{Grand})}{x.0 \;\dominion[0.5ex]{0.5em}{0.1ex}\hspace{-0.5em}\text{L}} = seven.58 \times 10^{-four} \;\text{atm}[/latex]

The total pressure is given by the sum of the fractional pressures:

[latex]P_\text{T} = P_{\text{H}_2} + P_\text{He} + P_\text{Ne} = (0.00632 + 0.00253 + 0.00076) \;\text{atm} = 9.61 \times 10^{-3} \;\text{atm}[/latex]

Check Your Learning
A 5.73-L flask at 25 °C contains 0.0388 mol of North_two, 0.147 mol of CO, and 0.0803 mol of H_ii. What is the total pressure in the flask in atmospheres?

Here is some other case of this concept, but dealing with mole fraction calculations.

Case 5

The Pressure of a Mixture of Gases
A gas mixture used for anesthesia contains ii.83 mol oxygen, O_ii, and 8.41 mol nitrous oxide, N_twoO. The total pressure level of the mixture is 192 kPa.

(a) What are the mole fractions of O₂ and N₂O?

(b) What are the fractional pressures of O₂ and North_iiO?

Solution
The mole fraction is given past [latex]X_A = \frac{n_A}{n_{Total}}[/latex] and the partial pressure level is [latex]P_A = X_A \times P_{Total}[/latex].

For O₂,

[latex]X_{O_2} = \frac{n_{O_2}}{n_{Total}} = \frac{two.83 \;\text{mol}}{(2.83 + 8.41) \;\text{mol}} = 0.252[/latex]

and [latex]P_{O_2} = X_{O_2} \times P_{Total} = 0.252 \times 192 \;\text{kPa} = 48.4 \;\text{kPa}[/latex]

For N₂O,

[latex]X_{N_2} = \frac{n_{N_2}}{n_{Total}} = \frac{eight.41 \;\text{mol}}{(ii.83 + viii.41) \;\text{mol}} = 0.748[/latex]

and

[latex]P_{N_2} = X_{N_2} \times P_{Total} = 0.748 \times 192 \;\text{kPa} = 143.6 \;\text{kPa}[/latex]

Check Your Learning
What is the force per unit area of a mixture of 0.200 k of H₂, 1.00 thou of N₂, and 0.820 grand of Ar in a container with a volume of ii.00 L at twenty °C?

Collection of Gases over Water

A simple way to collect gases that practice not react with water is to capture them in a bottle that has been filled with water and inverted into a dish filled with h2o. The pressure of the gas inside the bottle tin can exist made equal to the air pressure outside past raising or lowering the bottle. When the water level is the aforementioned both inside and outside the bottle (Figure 3), the pressure level of the gas is equal to the atmospheric pressure, which tin can be measured with a barometer.

Effigy 3. When a reaction produces a gas that is collected to a higher place water, the trapped gas is a mixture of the gas produced by the reaction and h2o vapor. If the collection flask is appropriately positioned to equalize the water levels both within and outside the flask, the pressure of the trapped gas mixture will equal the atmospheric pressure level outside the flask (see the earlier discussion of manometers).

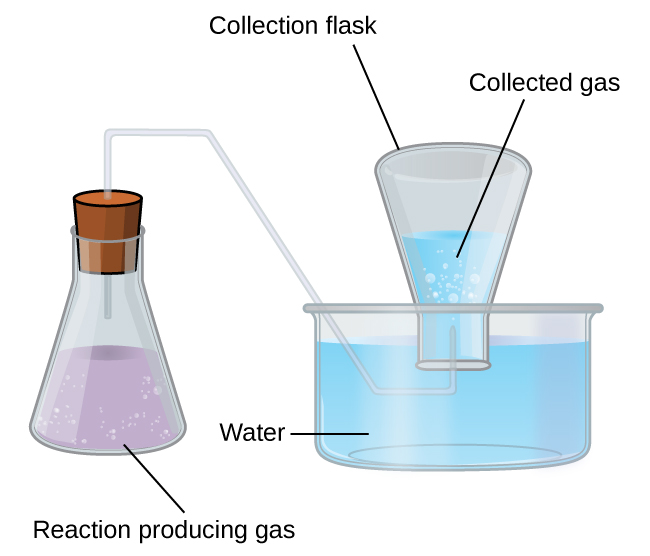
However, there is another factor we must consider when nosotros mensurate the pressure of the gas by this method. Water evaporates and there is always gaseous water (water vapor) above a sample of liquid water. Every bit a gas is collected over water, it becomes saturated with h2o vapor and the full pressure of the mixture equals the partial pressure of the gas plus the partial pressure level of the water vapor. The pressure of the pure gas is therefore equal to the full force per unit area minus the pressure of the water vapor—this is referred to as the "dry" gas pressure level, that is, the pressure of the gas only, without water vapor. The vapor pressure of water, which is the pressure level exerted by h2o vapor in equilibrium with liquid h2o in a closed container, depends on the temperature (Effigy 4); more detailed information on the temperature dependence of water vapor can be found in Tabular array 2, and vapor pressure will be discussed in more detail in the adjacent chapter on liquids.

Figure 4. This graph shows the vapor pressure of water at sea level as a part of temperature.

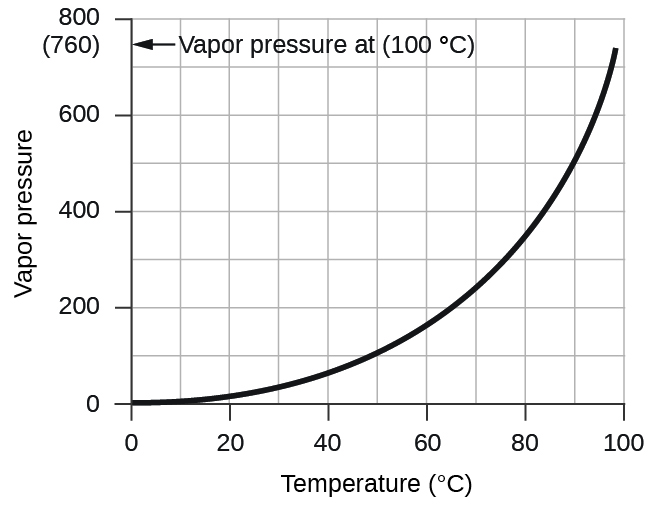
Temperature (°C)	Pressure (torr)		Temperature (°C)	Force per unit area (torr)		Temperature (°C)	Pressure (torr)
–x	1.95		eighteen	15.v		30	31.viii
–5	3.0		19	xvi.five		35	42.2
–ii	3.ix		20	17.5		twoscore	55.iii
0	4.6		21	18.7		fifty	92.5
ii	5.3		22	xix.8		60	149.4
4	six.1		23	21.1		70	233.7
half dozen	7.0		24	22.4		80	355.one
viii	eight.0		25	23.viii		90	525.8
ten	9.two		26	25.2		95	633.9
12	10.5		27	26.7		99	733.2
14	12.0		28	28.3		100.0	760.0
xvi	13.6		29	30.0		101.0	787.six
Tabular array 2. Vapor Pressure of Ice and Water in Various Temperatures at Sea Level

Instance vi

Pressure level of a Gas Collected Over Water
If 0.200 Fifty of argon is collected over water at a temperature of 26 °C and a pressure of 750 torr in a system like that shown in Effigy 3, what is the partial pressure of argon?

Solution
According to Dalton'southward law, the full pressure level in the bottle (750 torr) is the sum of the partial force per unit area of argon and the partial pressure of gaseous water:

[latex]P_\text{T} = P_\text{Ar} + P_{{\text{H}_2}\text{O}}[/latex]

Rearranging this equation to solve for the pressure level of argon gives:

[latex]P_\text{Ar} = P_\text{T} - P_{{\text{H}_2}\text{O}}[/latex]

The pressure of water vapor above a sample of liquid water at 26 °C is 25.2 torr (Appendix Eastward), so:

[latex]P_\text{Ar} = 750 \;\text{torr} - 25.ii \;\text{torr} = 725 \;\text{torr}[/latex]

Bank check Your Learning
A sample of oxygen collected over water at a temperature of 29.0 °C and a pressure level of 764 torr has a book of 0.560 L. What volume would the dry oxygen have nether the same conditions of temperature and force per unit area?

Chemical Stoichiometry and Gases

Chemical stoichiometry describes the quantitative relationships between reactants and products in chemic reactions.

We have previously measured quantities of reactants and products using masses for solids and volumes in conjunction with the molarity for solutions; now we can also use gas volumes to indicate quantities. If we know the volume, pressure, and temperature of a gas, we can use the ideal gas equation to calculate how many moles of the gas are nowadays. If we know how many moles of a gas are involved, we can summate the volume of a gas at any temperature and pressure level.

Avogadro'southward Police Revisited

Sometimes nosotros can take advantage of a simplifying characteristic of the stoichiometry of gases that solids and solutions exercise non showroom: All gases that testify platonic behavior contain the same number of molecules in the same volume (at the same temperature and pressure). Thus, the ratios of volumes of gases involved in a chemical reaction are given by the coefficients in the equation for the reaction, provided that the gas volumes are measured at the same temperature and pressure.

We can extend Avogadro'due south police force (that the volume of a gas is straight proportional to the number of moles of the gas) to chemical reactions with gases: Gases combine, or react, in definite and simple proportions past volume, provided that all gas volumes are measured at the aforementioned temperature and pressure. For example, since nitrogen and hydrogen gases react to produce ammonia gas according to [latex]\text{N}_2(grand) + iii\text{H}_2(g) \longrightarrow two\text{NH}_3(k)[/latex], a given volume of nitrogen gas reacts with iii times that volume of hydrogen gas to produce two times that book of ammonia gas, if pressure and temperature remain abiding.

The explanation for this is illustrated in Figure v. According to Avogadro's law, equal volumes of gaseous Northward₂, H₂, and NH_iii, at the aforementioned temperature and pressure, comprise the same number of molecules. Considering one molecule of N_two reacts with iii molecules of H_ii to produce two molecules of NH_iii, the volume of H₂ required is three times the volume of N_two, and the volume of NH_iii produced is two times the volume of N₂.

Figure 5. 1 volume of N₂ combines with three volumes of H_ii to form two volumes of NH₃.

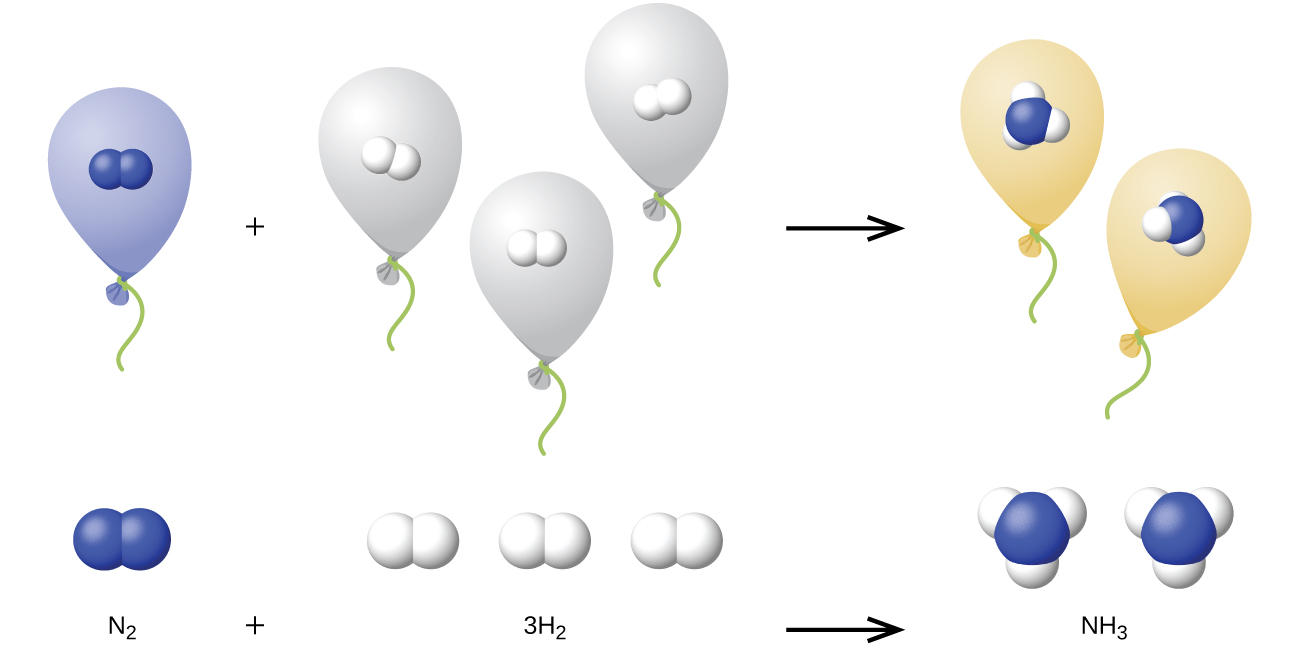
Example 7

Reaction of Gases
Propane, C₃H₈(g), is used in gas grills to provide the heat for cooking. What volume of O₂(g) measured at 25 °C and 760 torr is required to react with 2.vii L of propane measured under the same weather of temperature and pressure? Presume that the propane undergoes complete combustion.

Solution
The ratio of the volumes of C₃H₈ and O_ii will be equal to the ratio of their coefficients in the counterbalanced equation for the reaction:

[latex]\begin{assortment}{fifty c r} \text{C}_3 \text{H}_8(chiliad) + 5\text{O}_2(chiliad) & \longrightarrow & 3\text{CO}_2(m) + iv\text{H}_2 \text{O}(l) \\[1em] one \;\text{volume} + 5 \;\text{volumes} & & 3 \;\text{volumes} + four \;\text{volumes} \end{array}[/latex]

From the equation, we meet that one volume of C_threeH_viii will react with five volumes of O₂:

[latex]two.seven \;\rule[0.75ex]{3.2em}{0.1ex}\hspace{-three.2em}\text{L C}_3 \text{H}_8 \times \frac{five \;\text{L O}_2}{i \;\rule[0.35ex]{two.5em}{0.1ex}\hspace{-2.5em}\text{L C}_3 \text{H}_8} = thirteen.5 \;\text{L O}_2[/latex]

A volume of thirteen.5 50 of O₂ will be required to react with ii.seven 50 of C₃H_viii.

Check Your Learning
An acetylene tank for an oxyacetylene welding torch provides 9340 50 of acetylene gas, C_iiH₂, at 0 °C and 1 atm. How many tanks of oxygen, each providing vii.00 × 10^three L of O_two at 0 °C and one atm, will be required to burn the acetylene?

[latex]2\text{C}_2 \text{H}_2 + v\text{O}_2 \longrightarrow four\text{CO}_2 + two\text{H}_2 \text{O}[/latex]

Answer:

3.34 tanks (two.34 × 10⁴ Fifty)

Instance 8

Volumes of Reacting Gases
Ammonia is an important fertilizer and industrial chemical. Suppose that a volume of 683 billion cubic feet of gaseous ammonia, measured at 25 °C and 1 atm, was manufactured. What book of H₂(thou), measured nether the same atmospheric condition, was required to set up this amount of ammonia past reaction with N₂?

[latex]\text{Northward}_2(grand) + 3\text{H}_2(g) \longrightarrow ii\text{NH}_3(chiliad)[/latex]

Solution
Because equal volumes of H₂ and NH₃ incorporate equal numbers of molecules and each three molecules of H_two that react produce two molecules of NH₃, the ratio of the volumes of H₂ and NH_iii will exist equal to three:2. Ii volumes of NH₃, in this case in units of billion ft³, will exist formed from three volumes of H_ii:

[latex]683 \;\dominion[0.75ex]{vi.5em}{0.1ex}\hspace{-6.5em}\text{billion ft}^3 \;\text{NH}_3 \times \frac{3 \;\text{billion ft}^3 \;\text{H}_2}{two \;\rule[0.5ex]{iv.7em}{0.1ex}\hspace{-4.7em}\text{billion ft}^3 \;\text{NH}_3} = i.02 \times 10^3 \;\text{billion ft}^3 \;\text{H}_2[/latex]

The industry of 683 billion ft³ of NH₃ required 1020 billion ft³ of H₂. (At 25 °C and 1 atm, this is the volume of a cube with an edge length of approximately 1.9 miles.)

Check Your Learning
What volume of O_ii(g) measured at 25 °C and 760 torr is required to react with 17.0 L of ethylene, C_iiH₄(1000), measured under the same conditions of temperature and pressure level? The products are CO₂ and water vapor.

Example 9

Volume of Gaseous Production
What volume of hydrogen at 27 °C and 723 torr may be prepared past the reaction of 8.88 g of gallium with an excess of hydrochloric acid?

[latex]2\text{Ga}(s) + 6 \text{HCl}(aq) \longrightarrow 2\text{GaCl}_3 (aq) + 3\text{H}_2(yard)[/latex]

Solution
To catechumen from the mass of gallium to the book of H₂(g), we need to do something like this:

The showtime 2 conversions are:

[latex]8.88 \;\rule[0.75ex]{2.5em}{0.1ex}\hspace{-2.5em}\text{1000 Ga} \times \frac{i \;\rule[0.5ex]{ii.5em}{0.1ex}\hspace{-two.5em}\text{mol Ga}}{69.723 \;\rule[0.5ex]{ane.5em}{0.1ex}\hspace{-1.5em}\text{g Ga}} \times \frac{3 \;\text{mol H}_2}{2 \;\rule[0.5ex]{two.5em}{0.1ex}\hspace{-2.5em}\text{mol Ga}} = 0.191 \;\text{mol H}_2[/latex]

Finally, we tin can utilize the ideal gas police force:

[latex]V_{\text{H}_2} = (\frac{nRT}{P})_{\text{H}_2} = \frac{0.191 \;\rule[0.5ex]{1.25em}{0.1ex}\hspace{-i.25em}\text{mol} \times 0.08206 \;\text{Fifty} \;\rule[0.5ex]{4.5em}{0.1ex}\hspace{-iv.5em}\text{atm mol}^{-i} \text{Yard}^{-1} \times 300 \;\text{K}}{0.951 \;\rule[0.5ex]{1.4em}{0.1ex}\hspace{-1.4em}\text{atm}} = four.94 \;\text{L}[/latex]

Bank check Your Learning
Sulfur dioxide is an intermediate in the preparation of sulfuric acrid. What book of So₂ at 343 °C and 1.21 atm is produced by burning l.00 kg of sulfur in oxygen?

Greenhouse Gases and Climatic change

The thin skin of our temper keeps the earth from existence an ice planet and makes information technology habitable. In fact, this is due to less than 0.five% of the air molecules. Of the energy from the sun that reaches the earth, about [latex]\frac{ane}{3}[/latex] is reflected back into infinite, with the rest captivated by the atmosphere and the surface of the world. Some of the energy that the earth absorbs is re-emitted as infrared (IR) radiations, a portion of which passes dorsum out through the atmosphere into infinite. However, about of this IR radiations is captivated by certain substances in the atmosphere, known as greenhouse gases, which re-emit this energy in all directions, trapping some of the heat. This maintains favorable living conditions—without temper, the average global average temperature of xiv °C (57 °F) would be about –19 °C (–2 °F). The major greenhouse gases (GHGs) are h2o vapor, carbon dioxide, methane, and ozone. Since the Industrial Revolution, human activity has been increasing the concentrations of GHGs, which have changed the energy balance and are significantly altering the earth'southward climate (Figure 6).

Effigy 6. Greenhouse gases trap enough of the sun's free energy to make the planet habitable—this is known as the greenhouse effect. Homo activities are increasing greenhouse gas levels, warming the planet and causing more than extreme weather events.

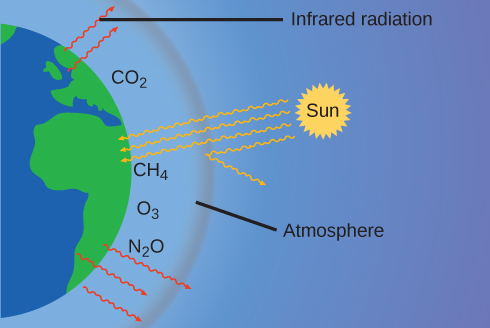
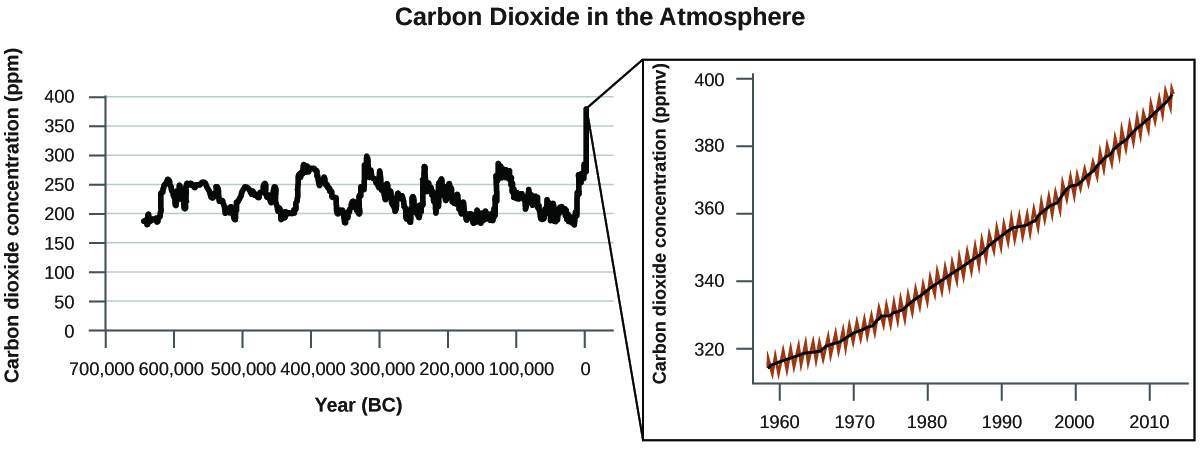
At that place is strong prove from multiple sources that higher atmospheric levels of CO_ii are caused by human activity, with fossil fuel called-for accounting for nigh [latex]\frac{iii}{4}[/latex] of the recent increase in CO₂. Reliable data from ice cores reveals that CO₂ concentration in the atmosphere is at the highest level in the by 800,000 years; other evidence indicates that it may be at its highest level in 20 meg years. In recent years, the CO_ii concentration has increased from historical levels of below 300 ppm to almost 400 ppm today (Figure seven).

Figure 7. CO_two levels over the past 700,000 years were typically from 200–300 ppm, with a steep, unprecedented increase over the by 50 years.

Click hither to see a 2-minute video explaining greenhouse gases and global warming.

Susan Solomon

Atmospheric and climate scientist Susan Solomon (Figure 8) is the writer of one of The New York Times books of the twelvemonth (The Coldest March, 2001), i of Fourth dimension magazine's 100 nigh influential people in the globe (2008), and a working group leader of the Intergovernmental Panel on Climate Change (IPCC), which was the recipient of the 2007 Nobel Peace Prize. She helped determine and explain the crusade of the formation of the ozone hole over Antarctica, and has authored many important papers on climatic change. She has been awarded the elevation scientific honors in the US and France (the National Medal of Science and the Grande Medaille, respectively), and is a member of the National Academy of Sciences, the Royal Society, the French Academy of Sciences, and the European University of Sciences. Formerly a professor at the Academy of Colorado, she is at present at MIT, and continues to work at NOAA.

For more than information, watch this video about Susan Solomon.

Figure 8. Susan Solomon's research focuses on climate change and has been instrumental in determining the cause of the ozone hole over Antarctica. (credit: National Oceanic and Atmospheric Administration)

Key Concepts and Summary

The ideal gas police can exist used to derive a number of user-friendly equations relating directly measured quantities to properties of interest for gaseous substances and mixtures. Appropriate rearrangement of the platonic gas equation may exist made to permit the calculation of gas densities and tooth masses. Dalton's police force of partial pressures may be used to relate measured gas pressures for gaseous mixtures to their compositions. Avogadro's police may be used in stoichiometric computations for chemical reactions involving gaseous reactants or products.

Key Equations

• [latex]P_{Total} = P_A + P_B + P_C + \cdots = \sum_\text{i} P_\text{i}[/latex]
• [latex]P_A = X_A P_{Total}[/latex]
• [latex]X_A = \frac{n_A}{n_{Total}}[/latex]

Chemistry End of Chapter Exercises

1. What is the density of laughing gas, dinitrogen monoxide, N₂O, at a temperature of 325 G and a pressure level of 113.0 kPa?
2. Calculate the density of Freon 12, CF_twoCl₂, at 30.0 °C and 0.954 atm.
3. Which is denser at the same temperature and pressure, dry out air or air saturated with h2o vapor? Explain.
4. A cylinder of O_ii(g) used in animate by emphysema patients has a volume of 3.00 L at a pressure of 10.0 atm. If the temperature of the cylinder is 28.0 °C, what mass of oxygen is in the cylinder?
5. What is the molar mass of a gas if 0.0494 chiliad of the gas occupies a volume of 0.100 Fifty at a temperature 26 °C and a pressure of 307 torr?
6. What is the molar mass of a gas if 0.281 g of the gas occupies a volume of 125 mL at a temperature 126 °C and a pressure of 777 torr?
7. How could yous show experimentally that the molecular formula of propene is C_iiiH_{half dozen}, non CH_ii?
8. The density of a sure gaseous fluoride of phosphorus is 3.93 g/Fifty at STP. Calculate the molar mass of this fluoride and determine its molecular formula.
9. Consider this question: What is the molecular formula of a compound that contains 39% C, 45% N, and sixteen% H if 0.157 g of the compound occupies l25 mL with a pressure level of 99.five kPa at 22 °C?

   (a) Outline the steps necessary to respond the question.

   (b) Answer the question.

10. A 36.0–L cylinder of a gas used for scale of blood gas analyzers in medical laboratories contains 350 g CO_ii, 805 g O₂, and 4,880 grand North₂. At 25 degrees C, what is the pressure in the cylinder in atmospheres?
11. A cylinder of a gas mixture used for calibration of blood gas analyzers in medical laboratories contains 5.0% CO₂, 12.0% O₂, and the balance N_ii at a total pressure of 146 atm. What is the partial pressure of each component of this gas? (The percentages given indicate the percent of the total pressure that is due to each component.)
12. A sample of gas isolated from unrefined petroleum contains ninety.0% CH_iv, eight.ix% C_twoH₆, and 1.one% C₃H₈ at a total pressure of 307.2 kPa. What is the fractional pressure of each component of this gas? (The percentages given indicate the percent of the total pressure that is due to each component.)
13. A mixture of 0.200 thousand of H₂, 1.00 g of N₂, and 0.820 g of Ar is stored in a closed container at STP. Observe the volume of the container, assuming that the gases showroom ideal beliefs.
14. Near mixtures of hydrogen gas with oxygen gas are explosive. All the same, a mixture that contains less than 3.0 % O₂ is not. If plenty O_ii is added to a cylinder of H₂ at 33.two atm to bring the full pressure to 34.5 atm, is the mixture explosive?
15. A commercial mercury vapor analyzer can discover, in air, concentrations of gaseous Hg atoms (which are poisonous) as depression as two × ten^−six mg/L of air. At this concentration, what is the partial pressure of gaseous mercury if the atmospheric pressure level is 733 torr at 26 °C?
16. A sample of carbon monoxide was collected over h2o at a total pressure level of 756 torr and a temperature of xviii °C. What is the pressure of the carbon monoxide? (Run across Table ii for the vapor pressure level of h2o.)
17. In an experiment in a full general chemistry laboratory, a student collected a sample of a gas over water. The volume of the gas was 265 mL at a pressure of 753 torr and a temperature of 27 °C. The mass of the gas was 0.472 yard. What was the molar mass of the gas?
18. Joseph Priestley first prepared pure oxygen by heating mercuric oxide, HgO:
    [latex]two \text{HgO}(due south) \longrightarrow 2\text{Hg}(l) + \text{O}_2(g)[/latex]

    (a) Outline the steps necessary to answer the following question: What book of O₂ at 23 °C and 0.975 atm is produced by the decomposition of 5.36 m of HgO?

    (b) Answer the question.

19. Cavendish prepared hydrogen in 1766 by the novel method of passing steam through a carmine-hot gun barrel:
    [latex]4 \text{H}_2 \text{O}(g) + iii\text{Iron}(s) \longrightarrow \text{Fe}_3 \text{O}_4 + 4\text{H}_2(1000)[/latex]

    (a) Outline the steps necessary to answer the post-obit question: What volume of H_ii at a pressure of 745 torr and a temperature of 20 °C can be prepared from the reaction of xv.O g of H₂O?

    (b) Answer the question.

20. The chlorofluorocarbon CCl_twoF₂ tin can be recycled into a different compound by reaction with hydrogen to produce CH₂F₂(thousand), a compound useful in chemical manufacturing:
    [latex]\text{CCl}_2 \text{F}_2(g) + four \text{H}_2(1000) \longrightarrow \text{CH}_2 \text{F}_2(thou) + two\text{HCl}(yard)[/latex]
    (a) Outline the steps necessary to answer the following question: What book of hydrogen at 225 atm and 35.v °C would be required to react with 1 ton (1.000 × ten³ kg) of CCl₂F₂?

    (b) Respond the question.

21. Automobile air bags are inflated with nitrogen gas, which is formed by the decomposition of solid sodium azide (NaN_iii). The other product is sodium metal. Calculate the volume of nitrogen gas at 27 °C and 756 torr formed by the decomposition of 125 g of sodium azide.
22. Lime, CaO, is produced by heating calcium carbonate, CaCO_three; carbon dioxide is the other production.

    (a) Outline the steps necessary to answer the following question: What volume of carbon dioxide at 875° and 0.966 atm is produced by the decomposition of one ton (one.000 × 10³ kg) of calcium carbonate?

    (b) Answer the question.

23. Before small batteries were available, carbide lamps were used for bicycle lights. Acetylene gas, C₂H_ii, and solid calcium hydroxide were formed by the reaction of calcium carbide, CaC₂, with water. The ignition of the acetylene gas provided the low-cal. Currently, the aforementioned lamps are used by some cavers, and calcium carbide is used to produce acetylene for carbide cannons.

    (a) Outline the steps necessary to reply the post-obit question: What volume of C₂H₂ at 1.005 atm and 12.two °C is formed by the reaction of 15.48 one thousand of CaC_two with h2o?

    (b) Answer the question.

24. Calculate the volume of oxygen required to burn 12.00 L of ethane gas, C₂H_half-dozen, to produce carbon dioxide and water, if the volumes of C₂H₆ and O_ii are measured under the same conditions of temperature and force per unit area.
25. What volume of O₂ at STP is required to oxidize 8.0 L of NO at STP to NO₂? What volume of NO_ii is produced at STP?
26. Consider the following questions:

    (a) What is the total volume of the CO₂(k) and H₂O(m) at 600 °C and 0.888 atm produced by the combustion of 1.00 L of C₂H₆(g) measured at STP?

    (b) What is the partial pressure of H_iiO in the product gases?

27. Methanol, CH₃OH, is produced industrially by the following reaction:[latex]\text{CO}(g) + ii \text{H}_2(yard) \xrightarrow{\;\;\;\;\;\;\text{copper goad} \;300 \;^{\circ} \text{C},\;300 \;\text{atm}\;\;\;\;\;\;} \text{CH}_3 \text{OH}(g)[/latex]
    Assuming that the gases behave equally platonic gases, find the ratio of the total volume of the reactants to the final volume.
28. What volume of oxygen at 423.0 K and a pressure of 127.iv kPa is produced by the decomposition of 129.7 g of BaO₂ to BaO and O₂?
29. A 2.l-L sample of a colorless gas at STP decomposed to give 2.50 L of N₂ and 1.25 L of O₂ at STP. What is the colorless gas?
30. Ethanol, C₂H_fiveOH, is produced industrially from ethylene, C₂H₄, by the following sequence of reactions:
    [latex]3 \text{C}_2 \text{H}_4 + ii\text{H}_2 \text{SO}_4 \longrightarrow \text{C}_2 \text{H}_5 \text{HSO}_4 + (\text{C}_2 \text{H}_5)_2 \text{SO}_4[/latex]
    [latex]\text{C}_2 \text{H}_5 \text{HSO}_4 + (\text{C}_2 \text{H}_5)_2 \text{And then}_4 + 3\text{H}_2 \text{O} \longrightarrow three\text{C}_2 \text{H}_5 \text{OH} + 2\text{H}_2 \text{So}_4[/latex]
    What volume of ethylene at STP is required to produce 1.000 metric ton (1000 kg) of ethanol if the overall yield of ethanol is 90.one%?
31. One molecule of hemoglobin volition combine with four molecules of oxygen. If 1.0 g of hemoglobin combines with ane.53 mL of oxygen at trunk temperature (37 °C) and a pressure of 743 torr, what is the molar mass of hemoglobin?
32. A sample of a compound of xenon and fluorine was confined in a bulb with a pressure of 18 torr. Hydrogen was added to the bulb until the pressure was 72 torr. Passage of an electric spark through the mixture produced Xe and HF. Afterwards the HF was removed past reaction with solid KOH, the final pressure of xenon and unreacted hydrogen in the bulb was 36 torr. What is the empirical formula of the xenon fluoride in the original sample? (Notation: Xenon fluorides contain only one xenon cantlet per molecule.)
33. One method of analyzing amino acids is the van Slyke method. The characteristic amino groups (−NH₂) in protein material are allowed to react with nitrous acid, HNO_two, to form N₂ gas. From the volume of the gas, the amount of amino acid can exist adamant. A 0.0604-g sample of a biological sample containing glycine, CH_ii(NH₂)COOH, was analyzed by the van Slyke method and yielded three.seventy mL of N_two collected over water at a pressure level of 735 torr and 29 °C. What was the percentage of glycine in the sample?
    [latex]\text{CH}_2 \; (\text{NH}_2) \text{CO}_2 \text{H} + \text{HNO}_2 \longrightarrow \text{CH}_2 \;(\text{OH}) \text{CO}_2 \text{H} + \text{H}_2 \text{O} + \text{N}_2[/latex]

Glossary

Dalton'due south law of partial pressures

total pressure of a mixture of ideal gases is equal to the sum of the partial pressures of the component gases.

mole fraction (X)

concentration unit defined as the ratio of the molar amount of a mixture component to the total number of moles of all mixture components

fractional pressure

pressure level exerted by an private gas in a mixture

vapor pressure level of water

pressure exerted by water vapor in equilibrium with liquid water in a airtight container at a specific temperature

Solutions

Answers to Chemical science End of Affiliate Exercises

two. 4.64 yard L⁻¹

4. 38.8 g

6. 72.0 thousand mol^−one

8. 88.1 yard mol⁻¹; PF₃

10. 141 atm

12. CH₄: 276 kPa; C₂H_{half dozen}: 27 kPa; C_threeH_eight: 3.four kPa

fourteen. Yes

16. 740 torr

18. (a) Determine the moles of HgO that decompose; using the chemical equation, determine the moles of O₂ produced by decomposition of this amount of HgO; and make up one's mind the volume of O₂ from the moles of O_ii, temperature, and pressure. (b) 0.308 L

xx. (a) Decide the molar mass of CCl₂F_two. From the balanced equation, summate the moles of H_two needed for the complete reaction. From the ideal gas law, catechumen moles of H_ii into book. (b) iii.72 × ten³ 50

22. (a) Remainder the equation. Determine the grams of CO_ii produced and the number of moles. From the ideal gas law, determine the volume of gas. (b) 7.43 × 10⁵ L

24. 42.00 50

26. (a) 18.0 L; (b) 0.533 atm

28. ten.57 L O₂

30. five.40 × ten⁵ L

32. XeF₂

---

furphydianstand1949.blogspot.com

Source: https://opentextbc.ca/chemistry/chapter/9-3-stoichiometry-of-gaseous-substances-mixtures-and-reactions/

Share :